Uso: Clasificador probabilístico de variables dicotómicas
Descripción: Tipo de análisis de regresión utilizado para predecir el resultado de una variable dicotómica. Este modelo resulta útil para modelar la probabilidad ocurrencia de un evento en función de otros factores.
Variable dependiente: no métrica (dicotómica)
Variables independientes: métricas y no métricas
Ejemplo en R: Clasificar si las piezas salen o no defectuosa atendiendo a la temperatura de la máquina.
# Cargar los datos para realizar el análisis
temperatura <-c(66,70,69,68,67,72,73,70,57,63,70,78,67,53,67,75,70,81,76,79,75,76,58)
defecto <-c( 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1)
aux <-matrix(c(temperatura,defecto),ncol = 2)
colnames(aux) <- c('temperatura','defecto')
datos<-data.frame(aux)
# Resumen de cuantos elementos hay de cada (tanto defectuosos como correctos)
table(datos$defecto)
## 0 1
## 18 5
# Representar visualmente los datos
colores <- NULL
colores[datos$defecto == 0] <- "green"
colores[datos$defecto == 1] <- "red"
plot(datos$temperatura, datos$defecto, pch = 21, bg = colores, xlab = "Temperatura", ylab = "Prob. defecto")
legend("bottomleft", c("No defecto", "Si defecto"), pch = 21, col = c("green", "red"))
# Ejecutar el modelo de regresión lineal generalizado y parametrizamos por binomial
reg <- glm(defecto ~ temperatura, data = datos, family = binomial)
summary(reg)
##
## Call:
## glm(formula = defecto ~ temperatura, family = binomial, data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.84513 -0.38010 -0.09632 -0.02831 2.41364
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 32.3381 17.6301 1.834 0.0666 .
## temperatura -0.5028 0.2643 -1.902 0.0571 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 24.0850 on 22 degrees of freedom
## Residual deviance: 9.8032 on 21 degrees of freedom
## AIC: 13.803
##
## Number of Fisher Scoring iterations: 7
# Dibujar la recta de probabilidad para cada una de las temperaturas
datos_probab <- data.frame(temperatura = seq(50, 85, 0.1))
datos.predict <- predict(reg, datos_probab, type = "response") # por defecto calcularía log p_i/(1-p_i), para calcular p_i usamos el argumento type
plot(datos$temperatura, datos$defecto, pch = 21, bg = colores, xlab = "Temperatura", ylab = "Prob. defecto")
legend("bottomleft", c("No defecto", "Si defecto"), pch = 21, col = c("green", "red"))
lines(datos_probab$temperatura, datos.predict, col = "blue", lwd = 2)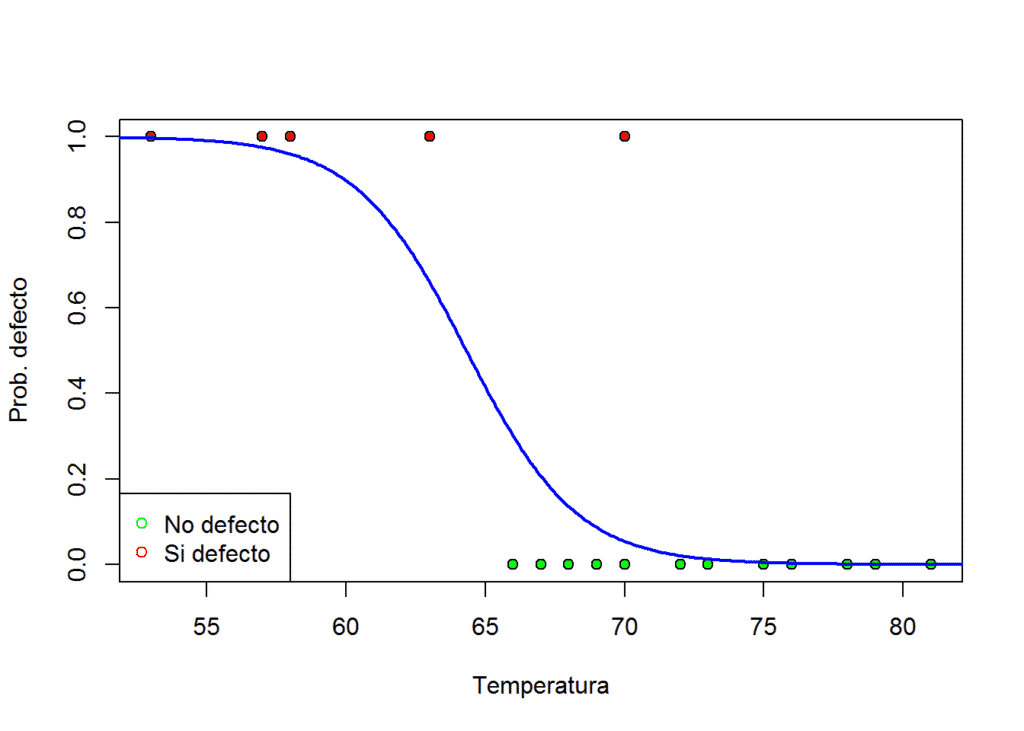
Predicción de pieza buena o defectuosa
#Predecimos la probabilidad de defectos y la insertamos en el dataframe como columna extra
datos$Fallo <- predict(reg,datos,type="response")
#Tomamos la decisión de si será defectuosa la pieza en función a su probabilidad de defecto
#Determinamos que la pieza será defectuosa cuando haya una probabilidad de defectos superior al 50%
datos$predic <- ifelse(datos$Fallo > 0.5,1,0)
#Enfrentamos la predicción contra la realidad
table(datos$predic,datos$defecto)
#Predecimos si una pieza es buena o defectuosa para una temperatura de 60ºC
Prob.def <- data.frame(temperatura=60)
Prediccion <- predict(reg, Prob.def, type = "response")
if (Prediccion >= 0.5) {
print("Pieza defectuosa")
}else{
print("Pieza buena")
}



Es muy claro el ejemplo que usan. Me podrían a guiar a replicar los gráficos con GGPLOT2?