Uso: Determinar si existe similitud entre grupos.
Objetivo: Compara si los valores de un conjunto de datos numéricos son significativamente distintos a los valores de otro conjunto de variables.
Variable dependiente: Métricas.
Variables independientes: Métricas
Ejemplo en R: Determinar si el pertenecer a un grupo u otro hace depender la influencia de las variables X sobre las Y.
# Generar una distribución normal aleatoria
set.seed(10)
valorX <- rnorm(50,0,1) # 50 valores de N(0,1)
valorY <- rnorm(50,0,10) # 50 valores de N(0,10)
valoresXY <- cbind(valorX,valorY) # 50 Coordinar los pares (x,y)
plot(valoresXY)# Realizar una rotación de los datos para mostrarlos como una regresión entre ambos valores
matriz_rotacion <- matrix(c(1,-1,1,1),nrow=2,ncol=2)
grupo1 <- valoresXY %*% matriz_rotacion # Rotar 45º
plot(grupo1)# Realizar el mismo proceso para el segundo grupo de datos
set.seed(11)
valorX <- rnorm(50,0,1) # 50 valores de N(0,1)
valorY <- rnorm(50,0,10) # 50 valores de N(0,10)
valoresXY <- cbind(valorX,valorY) # 50 Coordinar los pares (x,y)
grupo2 <- valoresXY %*% matriz_rotacion + 1 # Rotar 45º y cambiar por (1,1)
plot(grupo2)# Unir ambos grupos de datos en uno solo
grupos<-rbind(grupo1,grupo2)
# Identificar mediante factores cada uno de los 2 grupos
factores <- factor(c(rep("grupo1",50),rep("grupo2",50))) # Factores
# Pintar ambos grupos de diferentes colores. grupo1 = negro y grupo2 = rojo
blackred<-c(gl(2,50))
plot(grupos, col=blackred) # Blanco para el grupo1 y Rojo para el grupo2
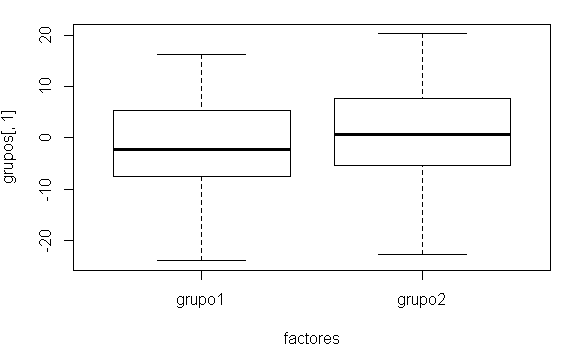
plot(grupos[,1], col=blackred) # Diagrama de dispersión de la primera coordenadaplot(grupos[,2], col=blackred) # Diagrama de dispersión de la segunda coordenadaplot(grupos[,1]~factores) # Diagrama de cajas de la primera coordenada
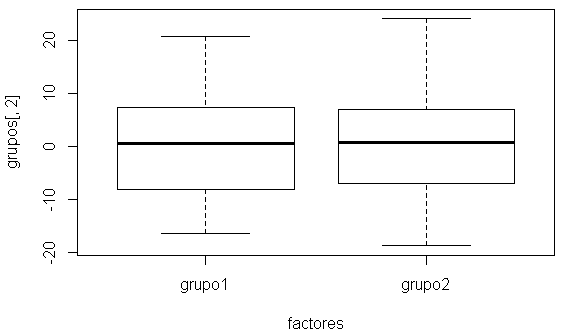
plot(grupos[,2]~factores) # Diagrama de cajas de la segunda coordenada # Ejecutar el modelo MANOVA para el conjunto de datos generado
modelo <- manova(grupos~factores)
# Mostrar los resultados como valores individuales mediante ANOVA
summary.aov(modelo)## Response 1 :
## Df Sum Sq Mean Sq F value Pr(>F)
## factores 1 46.9 46.919 0.4931 0.4842
## Residuals 98 9323.9 95.142
##
## Response 2 :
## Df Sum Sq Mean Sq F value Pr(>F)
## factores 1 13.9 13.865 0.1467 0.7025
## Residuals 98 9262.0 94.510# Se puede ver como los grupos de forma independiente son significativos ya que tienen un p-value mayor a 0,05
# Mostrar los resultados del modelo MANOVA para los datos de forma conjunta
summary.manova(modelo) ## Df Pillai approx F num Df den Df Pr(>F)
## factores 1 0.28101 18.955 2 97 1.125e-07 ***
## Residuals 98
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Se puede ver la unión de los grupos hace que las diferencias se conviertan en significativas p-value menor a 0,05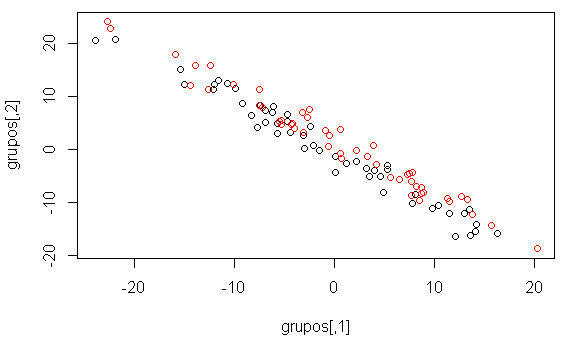




0 comentarios