Se muestra como calcular puntos outliers de un conjunto de datos utilizando los métodos de distancia de Gauss y distancia de Mahalanobis, para ello nos vamos a apoyar en el siguiente conjunto de datos:
# Cargar los datos ventas= c( 1054, 1057, 1058, 1060, 1061, 1060, 1061, 1062, 1062, 1064, 1062, 1062, 1064, 1056, 1066, 1070) clientes= c(63, 66, 68, 69, 68, 71, 70, 70, 71, 72, 72, 73, 73, 75, 76, 78) # Utilizamos la función data.frame() para crear un juego de datos en R datos <- data.frame(ventas ,clientes)
Método de distancia Estadística o de Gauss
El método de distancia estadística o de Gauss mejora el método clásico de distancia Eucliedea normalizando todas las variables bajo una misma escala [función en R: scale].
Ejemplo del cálculo de distancia estadística en R:
# Generar un vector boleano indicando los valores que esten a una distancia de más de 2 desviaciones estándar de la media ventas.outlier <- abs(scale(datos$ventas)) > 2 clientes.outlier <- abs(scale(datos$clientes)) > 2 # Almacenar los outlier encontrados para poder mostrarlos graficamente outlier <- rbind(datos[ventas.outlier ,], datos[clientes.outlier ,]) # Visualizar el gráfico con los datos destacando sus outlier plot(datos, pch=0) points(outlier , pch=16)
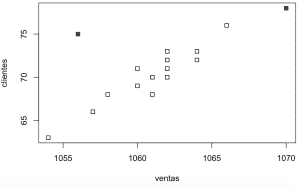
Método de distancia Mahalanobis
El método de distancia Mahalanobis mejora el método clásico de distancia de Gauss eliminando el efecto que pueden producir la correlación entre las variables a analizar. [función en R: mahalanobis].
Ejemplo del cálculo de distancia Mahalanobis en R:
# Determinar el número de outlier que queremos encontrar. num.outliers <- 2 # Ordenar los datos de mayor a menor distancia, según la métrica de Mahalanobis. mah.ordenacion <- order(mahalanobis(datos , colMeans( datos), cov(datos)), decreasing=TRUE) # Generar un vector boleano los dos valores más alejados segun la distancia Mahalanobis. outlier2 <- rep(FALSE , nrow(datos)) outlier2[mah.ordenacion[1:num.outliers]] <- TRUE # Resaltar con un punto relleno los 2 valores outliers. colorear.outlier <- outlier2 * 16 # Visualizar el gráfico con los datos destacando sus outlier. plot(datos , pch=0) points(datos , pch=colorear.outlier)
Método LOF – Local Outlier Factor
# Cargar paquete necesario para utilizar la función lofactor()
install.packages("lattice", dependencies = TRUE)
install.packages("grid", dependencies = TRUE)
install.packages("DMwR", dependencies = TRUE)
library(lattice)
library(grid)
library(DMwR)
# Datos a analizar
x1 <- rnorm(300, mean=8000, sd=1000)
y1 <- rnorm(300, mean=15, sd=200)
data.cluster <- data.frame(x1,y1)
# Calcular los outliers para un solo cluster
distancias.outliers <- lofactor(data.cluster , k=1)
# Dibujar la gráfica de frecuencias de distancias outliers
plot(density(distancias.outliers));
# Mostrar las distacicias para los 5 valores más alejados
outliers <- order(distancias.outliers , decreasing=T)[1:5]
print(outliers)
# Calcular todas las distancias de cada uno de los valores
distancias <- order(distancias.outliers , decreasing=T)[1:5]
# Mostrar todas las distancias de cada uno de los elementos para ver se ha fijado bien el número de outliers
plot(distancias.outliers[distancias])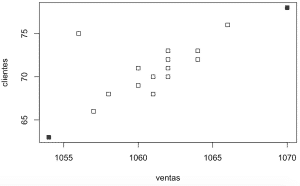




0 comentarios