Se va a llevar a cabo el desarrollo de un proyecto que nos permitiría predecir los fallos de una máquina industrial.
Para ello, será necesario un análisis de los datos, luego una transformación de los mismos para poder ser tratados
de forma óptima y finalmente se creará el modelo que permitirá hacer predicciones.
#Desactivamos notación científica
options(scipen=999) Carga de paquetes
Primero vamos a instalar y cargar las librerías necesarias, serán necesarios paquetes para manipular datos como dplyr y tidyr, para manipular fechas como lubridate, paquetes para explorar los datos como skimr y por último paquetes para realizar gráficos
#Instalar librerías
install.packages('dplyr')
install.packages('skimr')
install.packages('lubridate')
install.packages('tidyr')
install.packages('ggplot2')
#Cargar librerías
library(dplyr)
library(skimr)
library(lubridate)
library(tidyr)
library(ggplot2)Carga de datos
Después se procede a cargar los datos de un archivo que recoge las medidas más significativas cada día de una maquina a través de distintos sensores.
Fallos_maq <- read.csv(file = 'Fallos_de_Maquina.csv',sep=';')Análisis de datos
Posteriormente iremos con el análisis de los datos, en esta sección lo que haremos será llevar a cabo una visión general de los mismos con el objetivo de saber si hay medidas mal clasificadas, si encontramos valores atípicos, si hay medidas mas influyentes etc..
#Resumen general de los datos de cada medida extraída de los sensores de la máquina
glimpse(Fallos_maq)
#Visión más amplia de cada medida en la que se extraen los percentiles, maximo, mínimo,la media, desviación típica y hasta un histograma.
knitr::kable(skim(Fallos_maq)) 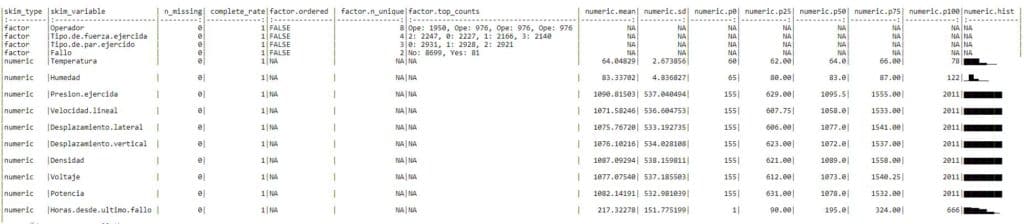
Se observa en la medida temperatura que tiene algun valor atípico dado que el mínimo y el percentil 25 se distancian en gran medida.
Para tener un mayor grado de análisis de esta variable vamos a aplicar la función ggplot que nos mostrará una gráfica con la que extrapolaremos si existen problemas con los datos recogidos en la misma, es decir, valores atípicos.
ggplot(Fallos_maq,x=1) + geom_boxplot(aes(y=Temperatura)) + ggtitle("Dispersión de los datos de temperatura") + theme_light()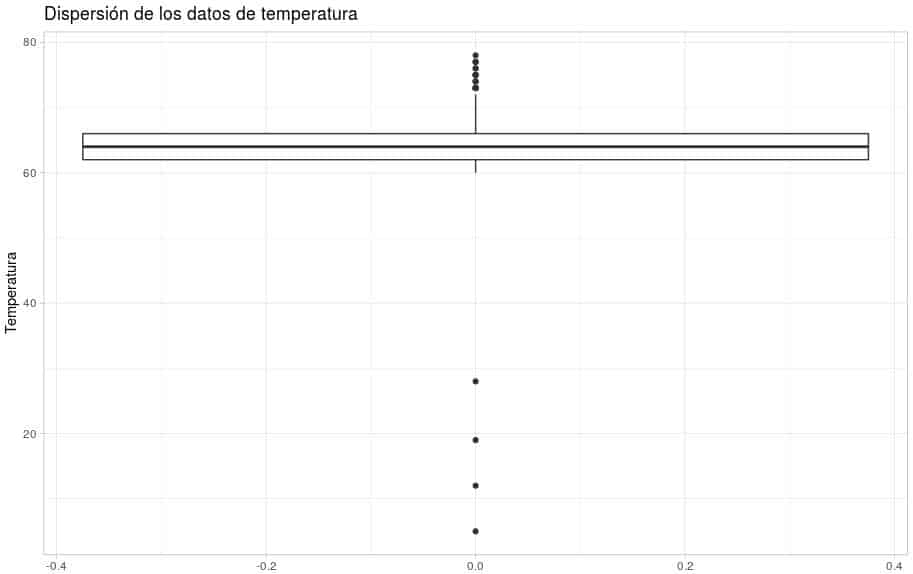
Se observan 4 valores aislados que no se corresponde con la relación del resto de datos.
Por tanto habrá que eliminar esos datos de nuestro modelo.
Por otro lado, podemos sacar en claro que en nuestras medidas que no existen valores nulos y tanto el tipo de fuerza ejercida como el tipo de par ejercido nos lo clasifica como un tipo de variable numérica, pudiéndose observar en los datos que se corresponde más con un tipo de variable factor ya que los datos recogidos van del 0 al 3, y 100% seguro que cada valor se corresponde con un tipo.
Por tanto será necesario hacer un cambio de variable.
Transformación de datos
Vamos con las correcciones mencionadas.
Fallos_maq <- Fallos_maq %>% #Usamos el simbolo %>% para que las acciones sucedan de forma consecutiva #guardando la anterior sentencia ejecutada
mutate(Tipo.de.fuerza.ejercida = as.factor(Tipo.de.fuerza.ejercida), #Cambiamos la variable de entero a factor
Tipo.de.par.ejercido = as.factor(Tipo.de.par.ejercido),
Fallo=as.factor(Fallo),
Operador=as.factor(Operador)) %>% #Cambiamos la variable de entero y caracter a factor
filter(Temperatura > 50) #Eliminamos los valores atípicos de la variable temperatura
#Observamos que las variables han cambiado
glimpse(Fallos_maq)
Análisis exploratorio de datos (EDA)
Vamos ahora con el analisis exploratorio de las variables (EDA), lo que vamos a conseguir es observar las correlaciones entre las variables, el balanceo de la variable objetivo y patrones raros que puedan surgir.
El concepto de balanceo lo que consigue es que exista un mínimo de datos de un tipo de resultado de una variable como para que el modelo pueda predecir con éxito.
Por ejemplo, si obtenemos solo 3 datos entre 1000 que dicen que «Si habrá fallo en la maquina», entonces el modelo se acomodará a predecir que «No existe fallo en la maquina» , es decir, que incluso cuando el resultado sea que «Sí existe fallo» , el modelo al haber tan pocos resultados de «Sí habra fallo en la maquina» se habrá acomodado a decir que «No existe fallo».
Por eso es tan importante realizar un balanceo si fuera necesario.
Vamos a realizar el analisis explotario en las variables de tipo factor primero y luego en las tipo entero esto es así porque vamos a emplear distintos gráficos para analizar cada tipo.
Posteriormente realizaremos un análisis de correlación entre todas las variables.
Finalmente observaremos el desbalanceo de la variable Fallo por si fuera necesario operar con su balanceo.
#Primero las de tipo factor
Fallos_maq %>%
select_if(is.factor) %>%
gather() %>% #Invierte filas y columnas para ayudar ggplot a realizar procesos más rapido
ggplot(aes(value)) + geom_bar(fill = rgb(0.2, 0.2, 1, 0.3), color = "blue") + facet_wrap(~key,scales='free') + theme_minimal()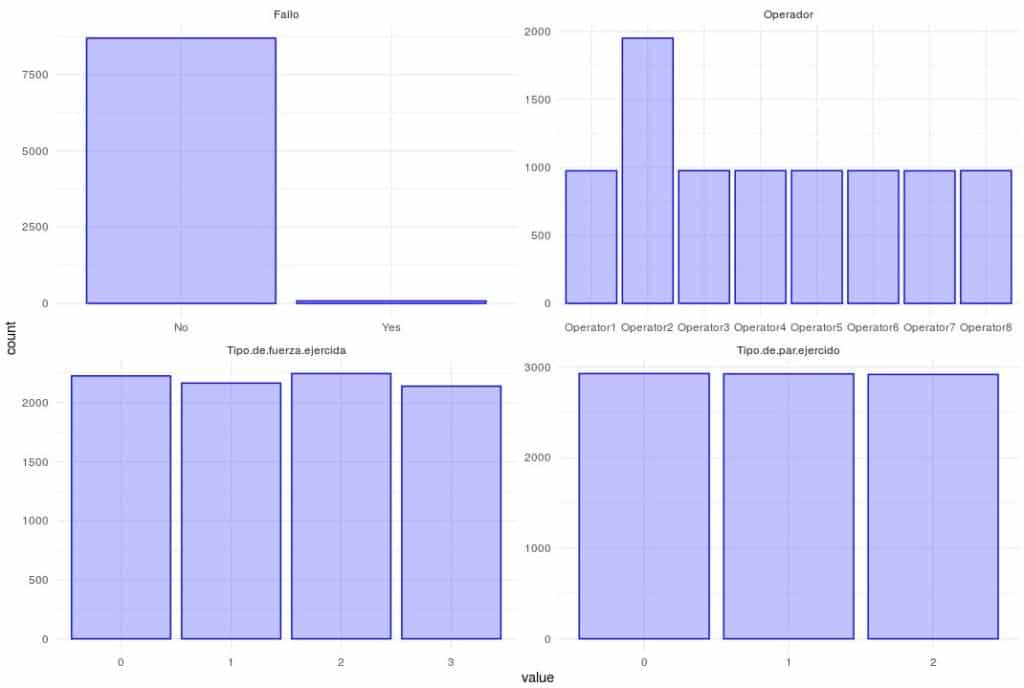
#Tipo entero
Fallos_maq %>%
select_if(is.integer) %>%
gather() %>%
ggplot(aes(value)) + geom_density(fill = rgb(0.2, 0.2, 1, 0.3), color = "blue") + facet_wrap(~key,scales='free') + theme_minimal() 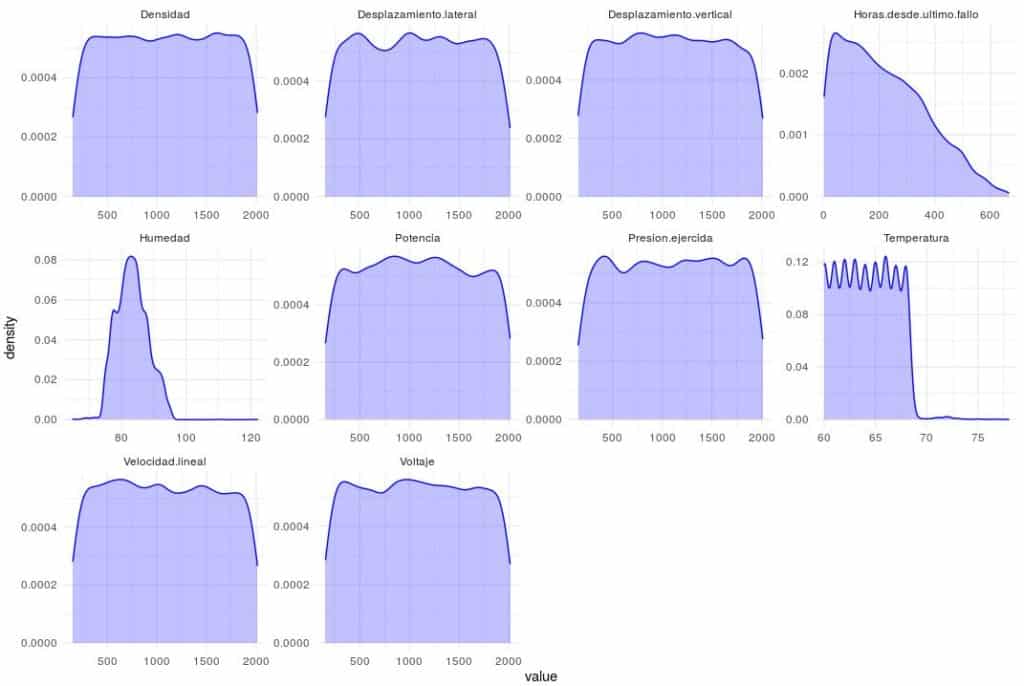
#A continuación vamos a realizar un análisis de correlación entre las distintas variables
Fallos_maq %>%
select_if(is.integer) %>%
cor() %>%
round(digits = 4)
#Observamos el desbalanceo de la variable Fallo
table(Fallos_maq$Fallo)
## No Yes
## 8699 81 No se perciben patrones raros en las variables.
Se observa que las variables de medida no se correlacionan dado que a mayor relación más cerca de 1, y observamos que solo hay 1 en la diagonal que evidentemente es la posición donde se cruza la misma variable.
Esto es positivo dado que no existirán problemas a la hora de predecir con nuestro modelo.
Finalmente se puede observar que la variable Fallo se encuentra desbalanceada dado que solo existen 81 «Si» frente a los 8699 «No». Por tanto habrá que corregir esta desviación con un balanceo de la variable.
Corregiremos el balanceo de las variables a continuación.
Transformación de variables
Tenemos dos técnicas para balancear un muestreo, inframuestreo y sobremuestreo, el inframuestreo reduce la parte de datos mayoritaria en este caso los «Si existe fallo», por otro lado el sobremuestreo genera datos artificiales (No reales) con el mismo patrón que los que había reales para no desviar el modelo, con el fin de aumentar los datos minoritarias de la proporción de resultados, en este caso los «No existe fallo».
Nos decantamos por emplear la técnica del inframuestreo.
#En primer lugar extraemos la proporción de "Si existe fallo"
81/nrow(Fallos_maq) * 100
## [1] 0.9225513
#Tenemos un 0,9% y necesitariamos mínimo un 10% para lograr un balanceo efectivo, por tanto
#Vamos a reducir la cantidad de "Si existe fallo" hasta que obtengamos una proporcion de 90%/10%.
set.seed(1234) #fijamos una semilla para obtener los mismos datos del ejercicio
Fallos_maq_NF <- Fallos_maq %>%
filter(Fallo == 'No') %>%
sample_frac(size = 0.08) #Extramos una fracción de 0,08% de los "No existe fallo" de esta manera,
#obtendremos la proporción deseada
Fallos_maq_SF <- Fallos_maq %>% filter(Fallo == 'Yes') #Extraemos un dataset con los "Si existe fallo"
#Unimos los dataset creados en un nuevo dataset que nos permita juntar los datos con las proporciones #adecuadas
Fallos_maq_Final <- rbind(Fallos_maq_NF,Fallos_maq_SF)
#Comprobamos el balanceo de las variables ahora
count(Fallos_maq_Final,Fallo)
## Fallo n
## 1 No 696
## 2 Yes 81
81/nrow(Fallos_maq_Final) * 100
## [1] 10.42471Hemos obtenido una proporción de los «No existe fallo» de un 10%, por tanto hemos terminado de balancear nuestro modelo de datos.
Es aconsejable aumentar más esta proporción de la variable minoritaria pero en este caso será suficiente.
Modelización
Nos metemos con la fase de modelización, en primer lugar vamos a dividir nuestro conjunto de datos en datos de entrenamiento del modelo y datos de validación.
#Extraemos el número de filas del dataset
tamano.total <- nrow(Fallos_maq_Final)
#Extrae el número que corresponde al 70% de las filas del Dataset
tamano.entreno <- round(tamano.total*0.7)
#Extrae el 70% de filas aleatorias del Dataset (solo el Nº de fila)
datos.indices <- sample(1:tamano.total , size=tamano.entreno)
#Extrae el 70% de las filas aleatorias anteriormente obtenidas del Dataset (datos de esas filas)
datos.entreno <- Fallos_maq_Final[datos.indices,]
#Extrae el 30% de filas restantes del Dataset (datos de esas filas)
datos.test <- Fallos_maq_Final[-datos.indices,]
#Comprobamos que no se haya desbalanceado el modelo de entrenamiento
count(datos.entreno,Fallo)
## Fallo n
## 1 No 487
## 2 Yes 57
81/nrow(datos.entreno) * 100
## [1] 14.88971Comprobamos que el modelo se ha balanceado incluso más, ahora tenemos cerca de un 15% en nuestra variable objetivo.
#Ahora vamos a extraer la variable Fallo que es la variable que queremos predecir
var_prediccion <- 'Fallo'
#Vamos a extraer las variables predictoras que serán las que nos permitan predecir si existe fallo o no, con #esto lo que conseguimos es extraer todas las variables quitando la variable predictora "Fallo".
var_predictoras <- names(datos.entreno)[-14] #la variable 14 es Fallo
#Creamos la fórmula que será la que el modelo de Machine Learning entiende cual será la que debe predecir y en función a que parámetros
form <- reformulate(var_predictoras,var_prediccion)Se usará l regresión logística para la modelización, este es un tipo de análisis de regresión utilizado para predecir el resultado de una variable dicotómica (Toma dos valores «Si» / «No»). Este modelo resulta útil para modelar la probabilidad ocurrencia de un evento en función de otros factores.
regresion <- glm(form,datos.entreno,family=binomial(link='logit'))
summary(regresion)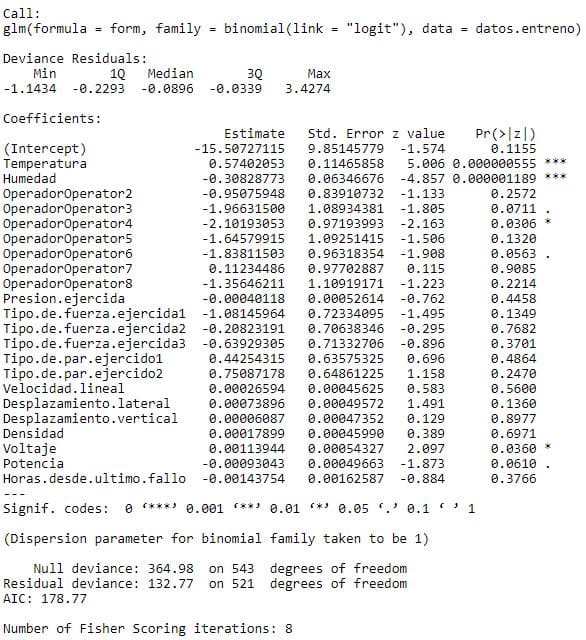
Analizamos el resumen del modelo predictivo y observamos que hay * en alguna variable, a cuantos más asteriscos haya mayor es la influencia predictiva de esa variale sobre la variable objetivo, en este caso la variable Fallo, con un * significa que la variable es predictiva al 95% mínimo. Vamos a obviar los asteriscos que haya en las categóricas como es Operador.
Vamos a crear un modelo con las variables mas predictivas.
var_predictoras_iter1 <- c('Temperatura','Humedad','Voltaje')
form <- reformulate(var_predictoras_iter1,var_prediccion) #actualizamos la fórmulaSe vuelve a crear el modelo de regresión logística.
regresion <- glm(form,datos.entreno,family=binomial(link='logit'))
summary(regresion)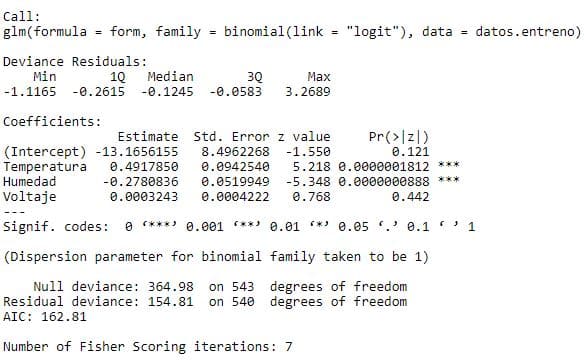
Se observa que la variable voltaje ahora no es significativa, solo lo son Temperatura y humedad, por tanto volvemos a crear un modelo con las variables más influyentes.
var_predictoras_iter2 <- c('Temperatura','Humedad')
form <- reformulate(var_predictoras_iter2,var_prediccion) #actualizamos la fórmulaSe volverá a crear el modelo de regresión logística.
regresion <- glm(form,datos.entreno,family=binomial(link='logit'))
summary(regresion)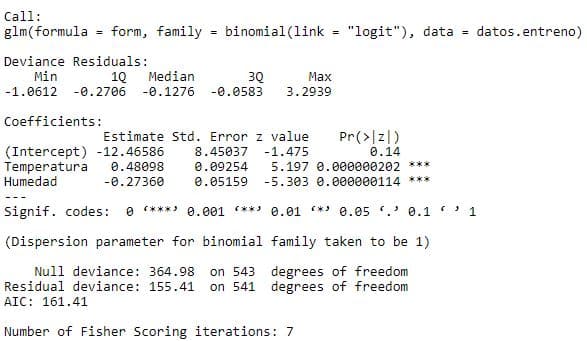
A continuación podemos comprobar como las 2 variables son influyentes y podemos validar nuestro modelo.
Evaluación del modelo
Se aplicarán los datos de validación para realizar las predicciones.
Predecimos la probabilidad de fallo y la insertamos en el dataframe de datos de validación como columna extra.
datos.test$probabilidad <- predict(regresion,datos.test,type='response')#Tomamos la decisión de si existirá fallo en la máquina en función a su probabilidad de fallo
#Determinamos que existirá fallo en la máquina cuando haya una probabilidad de fallo superior al 75%
datos.test$prediccion <- ifelse(datos.test$probabilidad > 0.75,1,0)Se contrastará la predicción contra la realidad mediante una matriz de confusión que sera la que me determine si la predicción ejecutada es buena.
mc <-table(datos.test$prediccion,datos.test$Fallo)
mc
## No Yes
## 0 209 10
## 1 0 14
# % correctamente clasificados
100 * sum(diag(mc)) / sum(mc)
## [1] 95.70815De mi predicción he acertado mas del 95% de los casos, vamos a ponernos en un caso en el que fuéramos menos restrictivos.
#Vamos a ver qué pasa si bajamos la decisión al 55%
datos.test$prediccion <- ifelse(datos.test$probabilidad > 0.55,1,0)
#Matriz de confusión para contrastar la predicción contra la realidad
mc <-table(datos.test$prediccion,datos.test$Fallo)
mc
## No Yes
## 0 208 8
## 1 1 16
# % correctamente clasificados
100 * sum(diag(mc)) / sum(mc)
## [1] 96.13734He aumentado mi capacidad predictiva a más de un 96%.




Hola Diego excelente tu articulo , es el primer artículo que veo que tiene aplicaciones más reales , me gustaría que podrías actualizar el link de la data para realizar el ejercicio.
Si no lo intentare con otra data para ver el resultado .
Gracias de antemano .